

This factor from the two polynomials means that unless this is a repeated factor of one of the polynomials, the resulting polynomials will no longer have 4Īs their root. This means that after factoring both polynomials, we can cancel this factor from the quotient. In the numerator and denominator of the quotient. In this case, the remainder theorem tells us that ( 𝑥 − 4 ) is a factor of the polynomials 𝑓 is a polynomial with 𝑓 ( 𝑎 ) = 0, then ( 𝑥 − 𝑎 ) is a factor of We recall the remainder theorem, which states that if We noted that both the numerator and denominator are equal to zero at 𝑥 = 4. This tells us we must use a different method to evaluate this limit. Is an indeterminate form, and it is not a valid answer to any limit problem. This means that our quotient takes the form 0 0 when we substitute the limit point. We can check this condition by substituting 𝑥 = 4 into the numerator:ģ × 4 − 1 8 × 4 + 2 4 = 4 8 − 7 2 + 2 4 = 0. If the numerator is not also equal to zero. In such a case, we know that the limit does not exist Since the denominator is equal to zero at the limit point, we cannot find this limit by direct substitution. We can check this condition by substituting the limit point 𝑥 = 4 into Only if the denominator does not equal zero at the limit point. We know that we can find the limit of a rational function by direct substitution In this example, we need to find the limit of a rational function. In our first example, we will consider a limit that takes the indeterminate form 0 0.Įxample 1: Finding the Limit of a Rational Function at a Pointįind l i m → 3 𝑥 − 1 8 𝑥 + 2 4 𝑥 − 1 6. When we notice that our limit takes an indeterminate form, we need toįind a different method to find this limit. It also does not mean that the limit does not exist or that we are unable to find the limit.

It cannot be overemphasized that the indeterminate form is not an answer to the limit problem. L i m → 𝑓 ( 𝑥 ) 𝑔 ( 𝑥 ) takes the indeterminate form 0 0. In particular, if 𝑓 ( 𝑥 )Īnd 𝑔 ( 𝑥 ) both approach zero as 𝑥 approaches 𝑎, we can say that the limit Instead, indeterminate forms mean that we cannot determine the value of the limit using that specific method. Indeterminate forms occur often when evaluating limits, but it is very important to keep in mind that an indeterminate form is never the final answer. We can compute a table of function values near the limit point 𝑥 = 0.Īn indeterminate form is an algebraic expression of numbers or infinity whose behavior cannot be determined in the current form. We can understand this better by considering a special case where 𝑓 ( 𝑥 ) = 1 𝑥 and 𝑎 = 0. This is because the quotient will become larger and larger in size (absolute value) if the denominator approaches zero Then we can say that this limit does not exist.

If the numerator 𝑓 ( 𝑥 ) does not approach zero near the limit point (i.e., l i m → 𝑓 ( 𝑥 ) ≠ 0), We cannot find such limits by direct substitution since substituting the limit point into the quotient will result in having a zero in the denominator. More specifically, we consider limits of the form In all of the limits that we will consider in this explainer, the functions will be in the form of a quotient so that the denominator is equal to zero at the limit point,Īnd thus the limit point will not lie in the domain. In this explainer, we will introduce an algebraic method of evaluating certain
#3 ways to find limits in calculus full
We can still use a table of values or the graph of the function to estimate the limit, but these methods usually requireĪ calculator to complete and often do not give us the full idea of the value of a limit. We cannot evaluate the limit by direct substitution. In other words, if the limit point does not belong to the domain of the function, This method is clearly invalid if the function is not defined at the limit point. In such cases, we can evaluate the limit by directly substituting the limit point into the function. While this distinction is very important to keep in mind, we know that, in many cases, the limit of a function is actually equal to the value of the function at the point.
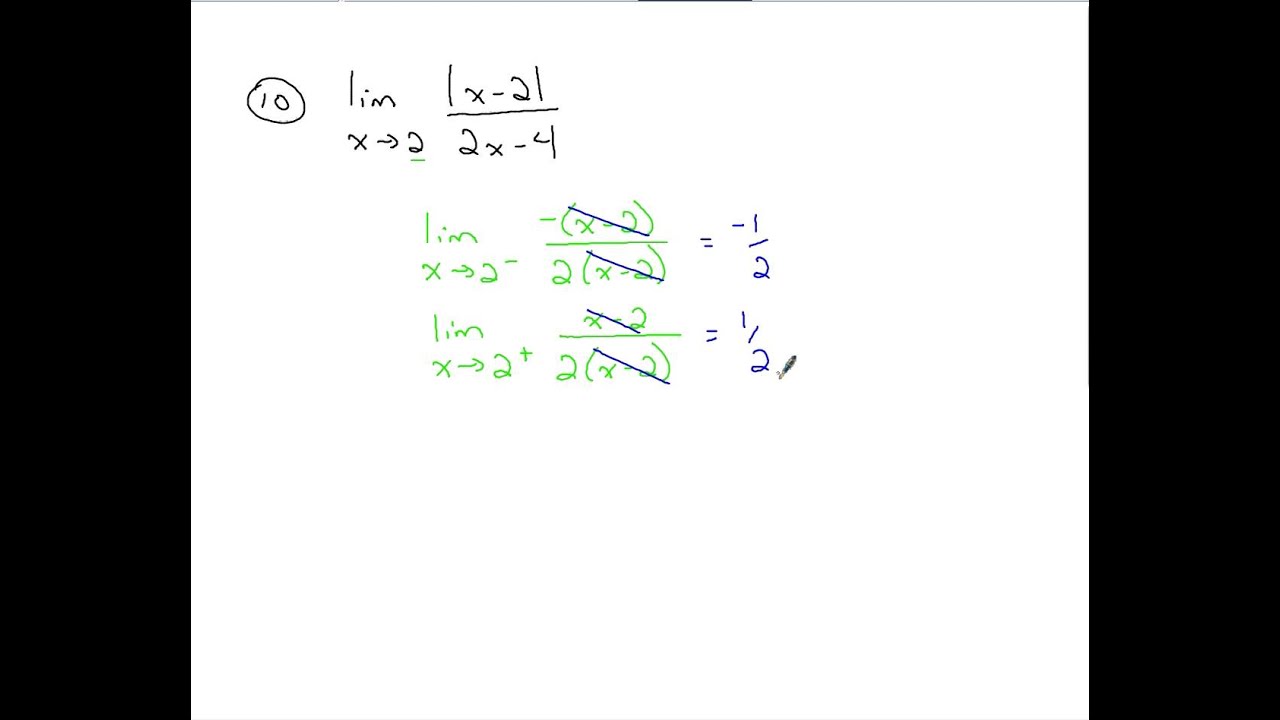
The limit of a function at a point describes the behavior of the function near the given point, rather than the value of the function at the point.
#3 ways to find limits in calculus how to
In this explainer, we will learn how to use algebraic techniques like factorization to evaluate limits.


 0 kommentar(er)
0 kommentar(er)
